火山喷发、地震、台风、泥石流等自然灾害以及爆炸、火箭发射、飞机飞行等人为事件均会产生频率低于20 Hz 的次声波,对这类次声波的研究有助于了解相关自然及人为事件的形成机制,实现灾害预警及事件跟踪。
声源的波达角度(Angle Of Arrivals, AOA) 定位问题实际是球面AOA的定位问题。球面AOA定位问题的传统解决方法主要包括球面三角定位法 (Spherical Triangulation, ST) 和最大似然估计器 (Maximum Likelihood Estimator, MLE)。ST算法通过计算球面示向线的交点来估计两个台站情况下的信源位置,是一种简单直观的方法,但是对于多台站的情况定位性能较差。MLE算法是最常用的球面AOA定位方法,受限于其迭代求解的特性,算法往往具有较高的计算复杂度。同时MLE算法需要谨慎选择初始估计,初值选择不慎易导致算法无法收敛。
为了解决上述问题,中国科学院声学研究所噪声与音频声学实验室的博士研究生张天予与其导师滕鹏晓研究员、吕君副研究员等人提出了一种球面加权伪线性估计器 (spherical weighted pseudo linear estimator, SWPLE),该算法可以求得次声源位置估计的准闭式解,避免了在MLE中常见的收敛性问题,具有更加稳健的性能,其计算复杂度也比传统算法更低。
为解决SWPLE算法存在的偏差问题,研究人员进一步提出了基于工具变量法的球面加权工具变量估计器 (spherical weighted instrumental variable estimator, SWIVE)。通过理论分析得到SWIVE算法具有渐近无偏性和渐近有效性,数值仿真证明了这一结论。该技术可为基于广域监测网的次声源定位需求及任务提供更加稳定快速的解决方案。
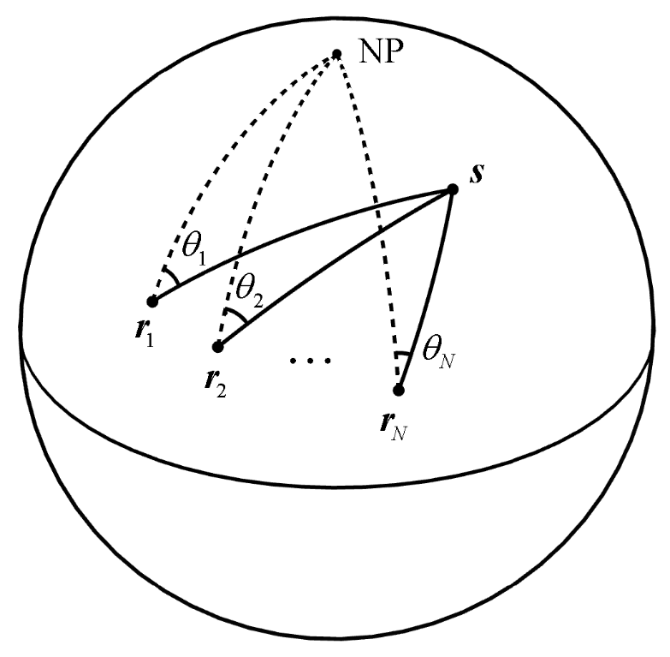
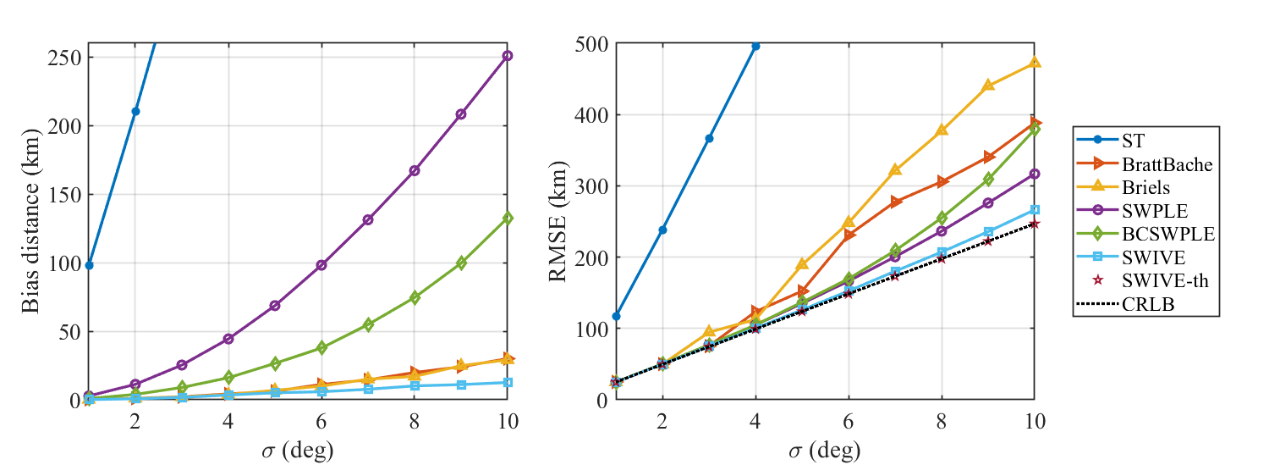
图2 独立同分布测量噪声下算法偏差距离和RMSE的对比(图/中国科学院声学研究所)
相关成果在线发表于国际信号处理期刊IEEE Transactions on Signal Processing。
本研究得到了国家自然科学基金 (No. 12174419) 的资助。
关键词:球面源定位,波达角度,伪线性估计器
参考文献:Zhang T, Teng P, Lyu J, et al. Quasi-closed-form algorithms for spherical angle-of-arrival source localization[J/OL]. IEEE Transactions on Signal Processing, 2024, 72: 432-448. DOI: 10.1109/TSP.2023.3340879.



